Estimation de l’affouillement en méandre : quelles formules dans quel contexte ? Application à la stabilisation des berges de rivières par le génie végétal
Lorsque les enjeux socio-économiques sont importants et ne peuvent être déplacés, des actions sont possibles pour limiter localement l’érosion naturelle des berges de cours d’eau. Les techniques de génie végétal apparaissent alors comme des solutions de protection à la fois efficaces, résilientes et favorables à la biodiversité. Cependant, leur durabilité peut être compromise par des processus naturels tel que l’affouillement qui correspond à un enfoncement localisé du lit qui advient au niveau d’un rétrécissement, d’une sinuosité ou d’un obstacle à l’écoulement. Bien que déterminant pour leur stabilité, ce processus est encore trop peu intégré dans le dimensionnement des ouvrages végétalisés. Cet article propose une synthèse inédite de onze formules d’estimation de profondeur d’affouillement en méandre issues de la littérature scientifique, et met à disposition un outil pratique pour accompagner les concepteurs dans une approche plus robuste et éclairée.
Introduction
Les érosions de berges sont des processus naturels, essentiels au bon fonctionnement des cours d’eau. En fournissant des matériaux hétérogènes, les érosions de berges jouent un rôle majeur dans l’équilibre morphologique des rivières et créent des écosystèmes rivulaires dynamiques et diversifiés. Par conséquent, la stabilisation systématique des berges peut aboutir à la chenalisation des rivières et entraîner un déficit sédimentaire conduisant à un enfoncement généralisé du lit.
Cette incision du lit mineur a des conséquences importantes : déstabilisation des berges et fragilisation par déchaussement des ouvrages d’art, abaissement des nappes et déconnexion des milieux. De nombreux services écosystémiques associés à la rivière ne sont alors plus fonctionnels. Pour éviter ce phénomène auquel il est extrêmement complexe de remédier, il est primordial de préserver l’espace de mobilité des cours d’eau et de recourir aux dispositifs de protection de berges uniquement lorsque les enjeux socio-économiques à protéger sont essentiels (Bonin et al., 2013).
Lorsqu’une protection s’impose, le génie végétal comme le génie civil, constituent un ensemble de techniques permettant la stabilisation des berges de cours d’eau. En génie végétal, c’est l’action de la végétation vivante qui stabilise les talus dans le temps principalement par le maintien du sol par les racines et le ralentissement des écoulements surfaciques par le système aérien (Gray et Sotir, 1996 ; Gyssels et al., 2005). Les techniques en végétal ont pour avantages de maintenir ou améliorer la biodiversité, le paysage et les services écosystémiques associés, sur des milieux particulièrement riches assurant des fonctions écologiques majeures.
Dans la pratique, ces techniques sont principalement dimensionnées empiriquement à dire d’expert et promues par retour d’expérience. La conception des ouvrages ne passe pas systématiquement par un calcul de stabilité face aux aléas pour lesquels ils sont dimensionnés. Les végétaux en tant que « vivants » sont soumis à une variabilité naturelle intrinsèque ainsi qu’aux influences du contexte environnemental. Ceci rend complexe la détermination de critères de dimensionnement quantitatifs et universels ainsi que l’utilisation de modèles numériques pour prévoir la tenue des ouvrages.
La variable quantitative d’appui à la conception que l’on retrouve principalement dans la littérature autour du génie végétal est la contrainte tractrice (Leblois et al., 2016). Telles que fournies dans les guides, ces valeurs ne sont qu’indicatrices et ne représentent ni un seuil d’acceptabilité maximale pour une technique donnée, ni ne permettent d’assurer de la tenue d’un ouvrage, ni ne sont pleinement représentatives du processus physique menant à la déstabilisation des ouvrages (Leblois et al., 2024). Il ressort cependant de ces valeurs que certaines techniques acceptent mieux des contextes à fortes contraintes tractrices que d’autres.
Compte tenu du manque de méthodes de dimensionnement pour le génie végétal qui soient quantitatives et qui viennent contrer les modes de défaillance des ouvrages, cette étude propose un outil permettant d’estimer les profondeurs d’affouillement attendues en méandre. En effet, ce phénomène constitue l’une des causes majeures de déstabilisation des ouvrages de génie végétal (Leblois et al., 2022). Sans un pied de berge tenu, l’ensemble de la berge tombe dans le lit. L’estimation de ces profondeurs a pour vocation de permettre au concepteur de choisir s’il faut mettre en place ou non des ouvrages en pied et sous la berge végétalisée afin de stabiliser celle-ci face à l’affouillement. L’estimation des profondeurs d’affouillement est ensuite nécessaire pour connaître la profondeur d’ancrage de ces ouvrages de pied de berge. Cette démarche offre une conception plus robuste des ouvrages de stabilisation de berge en génie végétal.
Description de l’affouillement et de ses effets sur les ouvrages en génie végétal
Définition
L’affouillement est un phénomène d’enfoncement du lit d’un cours d’eau qui résulte de processus hydrauliques et géomorphologiques naturels. Il se distingue de l’incision par son caractère ponctuel. Une incision est un phénomène plus global qui se traduit par un enfoncement du lit sur une distance significative (supérieure à des centaines de fois la largeur du cours d’eau), et entraînant ainsi des ajustements morphologiques majeurs (USDA et NRCS, 2007a)
En comparaison, l’affouillement est un phénomène plus localisé spatialement. Comme proposé par USDA et NRCS (2007b), il est possible de distinguer l’affouillement dit général qui impact une section transverse complète, d’un affouillement encore plus local. L’affouillement local correspond à un enfoncement du lit directement lié à une singularité : pile de pont, embâcles ou autre obstacle à l’écoulement. À l’inverse, l’affouillement général affecte souvent une partie importante voire l’entièreté de la section transversale du cours d’eau. Ce dernier est caractéristique des affouillements dus à un rétrécissement ou à la présence d’une sinuosité (USDA et NRCS, 2007b).
La profondeur d’affouillement totale dans une zone donnée peut ainsi être calculée en additionnant tous les types d’affouillement et l’incision présents sur le tronçon concerné (USDA et NRCS, 2007b). Cette étude se concentre uniquement sur la détermination de la profondeur d’affouillement apparaissant en extrados
Les formules présentées dans cet article permettent de calculer directement la profondeur d’affouillement en méandre (haff), qui peut se définir empiriquement par la différence entre la profondeur d’eau maximale dans le méandre (hmax) et la profondeur d’eau moyenne sur une section amont (hmoy, amont), équation (1).
haff = hmax- hmoy, amont (1)
Description du processus et de ses effets en méandres
Le processus d’érosion de berge peut se diviser en trois étapes successives (Thorne, 1982) : (1) charriage des matériaux non cohésifs présents en pied de berge (sables, graviers), ce qui entraîne un affouillement ; (2) effondrement des matériaux de la berge (sables, graviers mais aussi argiles, végétation) ; (3) transport de ces nouveaux matériaux puis reprise du cycle avec l’érosion des matériaux en pied de berge. Plus les contraintes tractrices exercées sur le fond du lit et les berges sont élevées, plus l’entraînement des matériaux par la rivière est important en phases (1) et (3) (en granulométrie comme en volume mobilisé). Ces contraintes augmentent notamment avec la pente du lit et la hauteur d’eau.
En extrados de méandre, l’érosion des berges est accrue. Des courants secondaires sont provoqués par la conjugaison d’une distribution verticale non uniforme des vitesses et la présence d’une courbure (Odgaard, 1989), figure 1. L’écoulement secondaire se met en place sous la forme hélicoïdale, sous les effets couplés des vitesses, plus importantes en surface qu’en fond de lit, et de la force centrifuge. Les courants secondaires se développent perpendiculairement à la direction du courant principal qui suit la ligne d’énergie : les écoulements plongent en extrados et remontent en intrados. En conséquence, ces courants provoquent un tri granulométrique avec le déplacement latéral du méandre vers l’extrados et des dépôts en intrados (Matsuura, 2004 ; Julien, 2018).
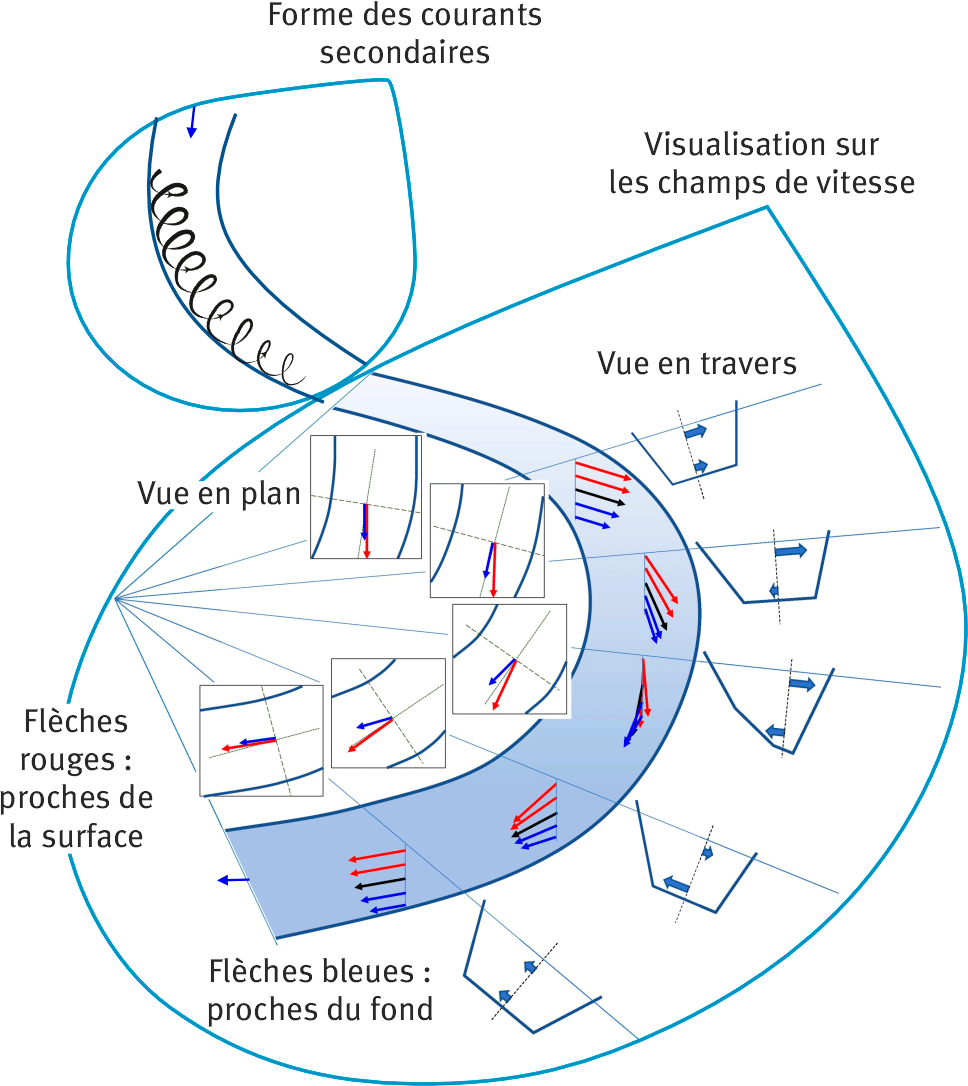
Figure1. Description du processus d’affouillement en méandre : forme des courants secondaires et répartition des vitesses d’écoulement (modifié d’après Somsook et al. (2020) et Bates (2022).
Ces mouvements ont pour effet d’augmenter localement la contrainte tractrice et donc l’entraînement des matériaux de l’extrados (Papanicolaou et al., 2007). Julien (2018) propose l’équation (2) pour estimer la contrainte tractrice maximale en méandre (τ méandre en N/m2). L’équation s’appuie sur la contrainte tractrice appliquée au fond du lit en chenal rectiligne (τ en N/m²), avec : ρ (kg/m3), la masse volumique du fluide ; g (9,81 m/s²), l’accélération gravitationnelle ; Rh (m), le rayon hydraulique (surface mouillée/périmètre mouillé) ; i (m/m) la pente moyenne du cours d’eau ; L (m), la largeur de la rivière ; et Rc (m), le rayon de courbure du méandre.
τ méandre = τ·(1+2∙L/Rc ) avec τ = ρ·g·Rh·i (2)
La ligne d’eau en extrados subit une surélévation et le niveau en intrados une sous-élévation de même amplitude (USDA et NRCS, 2007a ; Blanchet et Morin, 1990). En régime fluvial, ΔZ (m), la surélévation en extrados par rapport au niveau moyen relevé à l’axe central de la rivière dépend de la vitesse moyenne dans le chenal au carré (V en m/s) et peut se calculer à l’aide de l’équation (3). Suivant la source littéraire, l’équation est appliquée avec un coefficient C de valeur variable entre 1 et 2 (Blanchet et Morin, 1990). La valeur de ce coefficient C étant difficile à fixer, le résultat de l’équation est souvent utilisé avec un coefficient de sécurité.
∆Z = (L∙V2)/(2∙g∙Rc ) (3)
L’axe longitudinal de développement de l’affouillement en méandre est précisé dans l’encadré 1.
En méandre, l’affouillement maximal est localisé à partir du secteur C présenté sur la figure ci-contre (Blanchet et Morin, 1990 ; USDA et NRCS, 2007b).
Le début du secteur C est déterminé par le point où la tangente, issue de la berge d’intrados avant le début du méandre, vient rencontrer l’extrados (pointillés sur la figure ci-dessous).
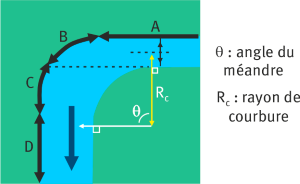
L’érosion aux extrémités des ouvrages et par contournement est la troisième cause mécanique de défaillance des ouvrages en génie végétal (Leblois et al., 2022). Les techniques de protection doivent de fait couvrir les secteurs de B à D à minima afin d’assurer la continuité de la protection (tableau ci-dessous).
Zone | Angle d’attaque du courant dans la berge | Affouillement | Positionnement de la protection |
A | Parallèle – 0° à 10° | Faible | - |
B | Modéré – 10° à 45° | Modéré | Début de la protection |
C | Frontal – 45° à 90° | Fort | Protection renforcée |
D | Parallèle – 0° à 10° | Modéré | Fin de la protection |
Modifié d’après AMEC (2012). | |||
Rôle de l’affouillement dans la défaillance des ouvrages en génie végétal
Sur la base d’observations en méandres sur modèle réduit, le principal processus de défaillance mécanique d’un ouvrage de génie végétal, comme une fascine de pied de berge, peut se décomposer en trois étapes : (1) création d’une fosse d’affouillement sous l’ouvrage ; (2) chute des matériaux de berge situés derrière l’ouvrage dans la fosse ; (3) transport des matériaux tombés dans la fosse vers l’intrados et vers l’aval (Leblois et al., 2024).
D’après une analyse des ouvrages de la base de données GeniVeg (Jaymond et al., 2021), sur un échantillon de 170 ouvrages défaillants, 45 % étaient concernés par l’affouillement (Leblois et al., 2022). Sur un échantillon de 470 fascines de pied de berge tout état confondu, 9 % étaient concernées par l’érosion en pied. Après la mauvaise reprise de la végétation, l’affouillement est la première cause de dégradation d’un ouvrage, observée sur 13 % de l’échantillon de fascines (Leblois et al., 2024). De surcroît, le phénomène d’affouillement induit une mauvaise reprise de végétation. En effet, sans contact avec le substrat du sol, les végétaux ne peuvent pas se développer de manière pérenne et stabiliser durablement les ouvrages.
La grande majorité des ouvrages de génie végétal dont ceux analysés par Leblois et al., 2022, 2024) n’intègrent pas d’éléments de stabilisation sous le niveau de reprise de la végétation et n’ont pas été dimensionnés pour faire face à l’incision ou à l’affouillement potentiel du site. Or, l’absence ou la mauvaise évaluation du risque d’affouillement constitue un défaut majeur et connu de conception qui conduit à de nombreuses ruptures d’ouvrages de protection de berge (USDA et NRCS, 2007c).
De façon cohérente avec ces considérations, une expérimentation menée sur des saules âgés de deux à cinq ans a montré que la force nécessaire pour les arracher est cinq à dix fois supérieure à la force de traînée exercée par le courant sur le système aérien (Bonin et al., 2013 ; Vollsinger et al., 2000). Cette force nécessaire à l’arrachement est également supérieure d’un ordre de grandeur aux contraintes tractrices estimées en crue au droit d’ouvrages en génie végétal (Leblois et al., 2016). Ainsi la force engendrée par le courant et appliquée à la partie aérienne des végétaux, ne suffit pas à expliquer la défaillance des ouvrages. En revanche, suite à la mobilisation des matériaux en pied de berge déchaussant le système racinaire, les forces provoquées par l’écoulement et appliquées à la végétation et au fond du lit peuvent déstabiliser la végétation rivulaire et les ouvrages de génie végétal (Edmaier et al., 2011).
Formules existantes
Historique
De nombreux guides de dimensionnement d’ouvrages de protection de berges par des méthodes de génie civil existent (enrochements libres versés, enrochements libres agencés, enrochements liés au béton, enrochements liés avec des chaînes, murs en béton…). Ces guides présentent des critères calculatoires de conception, ainsi que les différents facteurs à prendre en compte, pour assurer la bonne tenue des ouvrages et éviter leur rupture. Sans surprise, l’affouillement y est régulièrement évoqué. Des formules analytiques ou empiriques sont proposées afin d’évaluer les profondeurs sollicitées. Ces connaissances sont encore peu transférées vers le génie végétal.
Les premières formules, pour évaluer les profondeurs d’affouillement, recensées dans cet article datent de 1930 et ont été développées par Lacey. Cet auteur a étudié le phénomène d’affouillement pour définir les caractéristiques de canaux d’irrigation en Inde. Son travail a ensuite été repris par différents auteurs. En France, la crue de 1957 sur l’Arc (Savoie) a motivé le ministère des Travaux Publics à mettre en œuvre une étude générale sur l’affouillement en méandre dans les rivières à fortes pentes. Cette étude conduite par SOGREAH, s’appuie sur des travaux réalisés en modèle réduit. Aux États-Unis, dans les années 1980 et 1990, des chercheurs, de l’U.S. Army Corps of Engineers ont également développé plusieurs formules à partir d’expériences en laboratoire et de mesures réalisées sur des grandes rivières à méandres. Toutes les formules présentées sont empiriques sauf celle de Zeller qui est analytique.
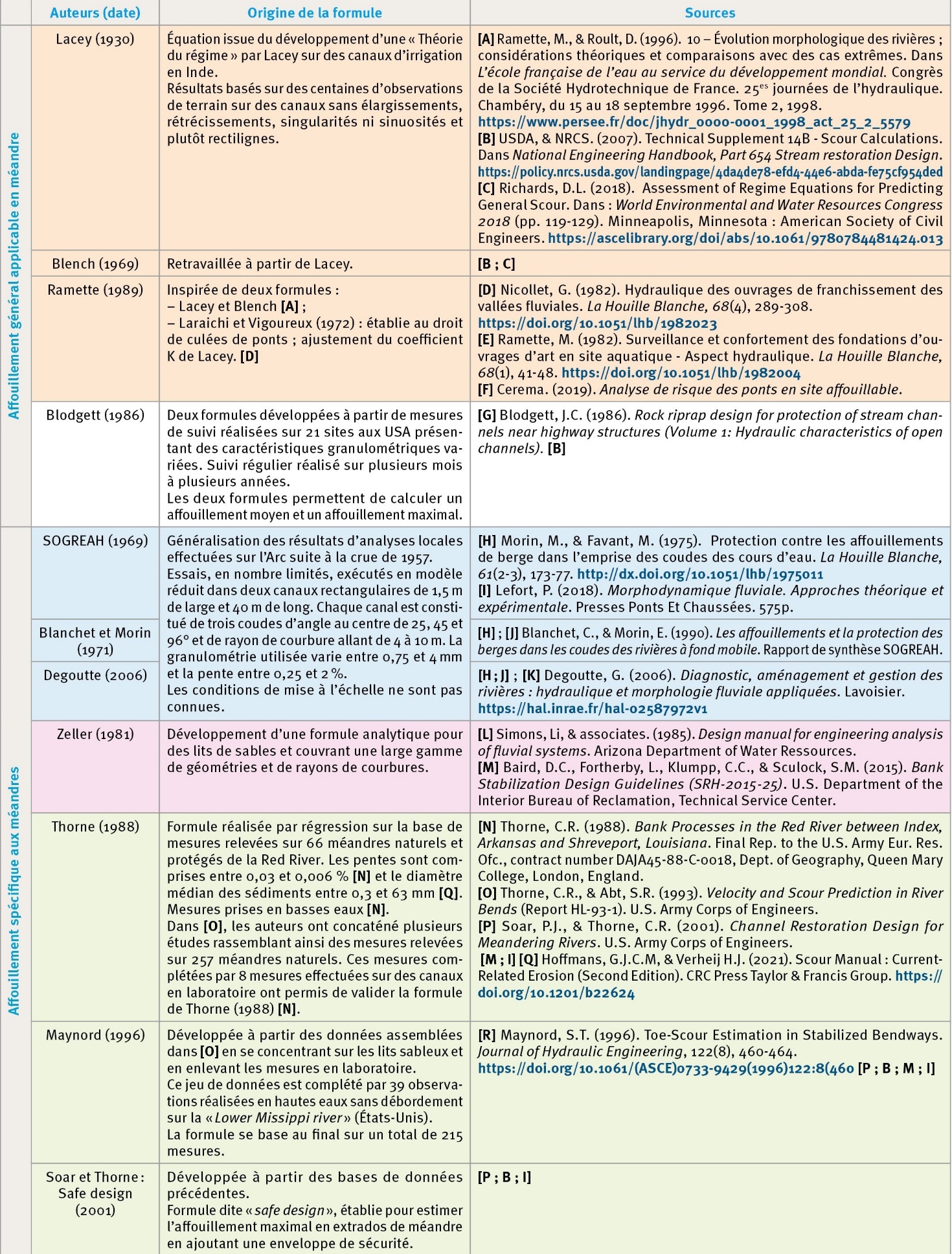
Le tableau 1 présente une synthèse de la provenance des onze formules de calcul d’affouillement et les références bibliographiques associées. Chaque couleur correspond à un groupe de formules inspirées les unes des autres.
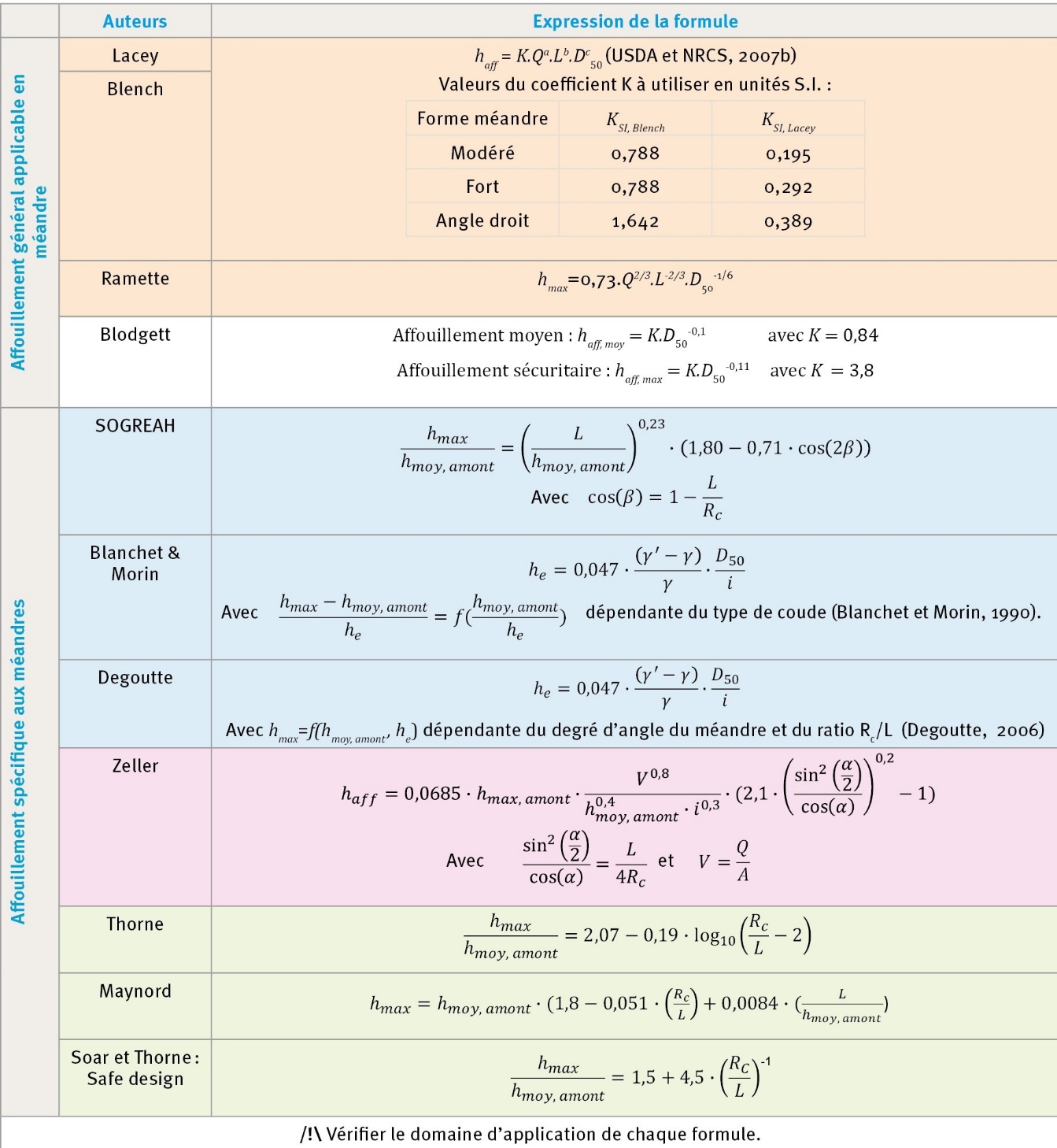
Les formules
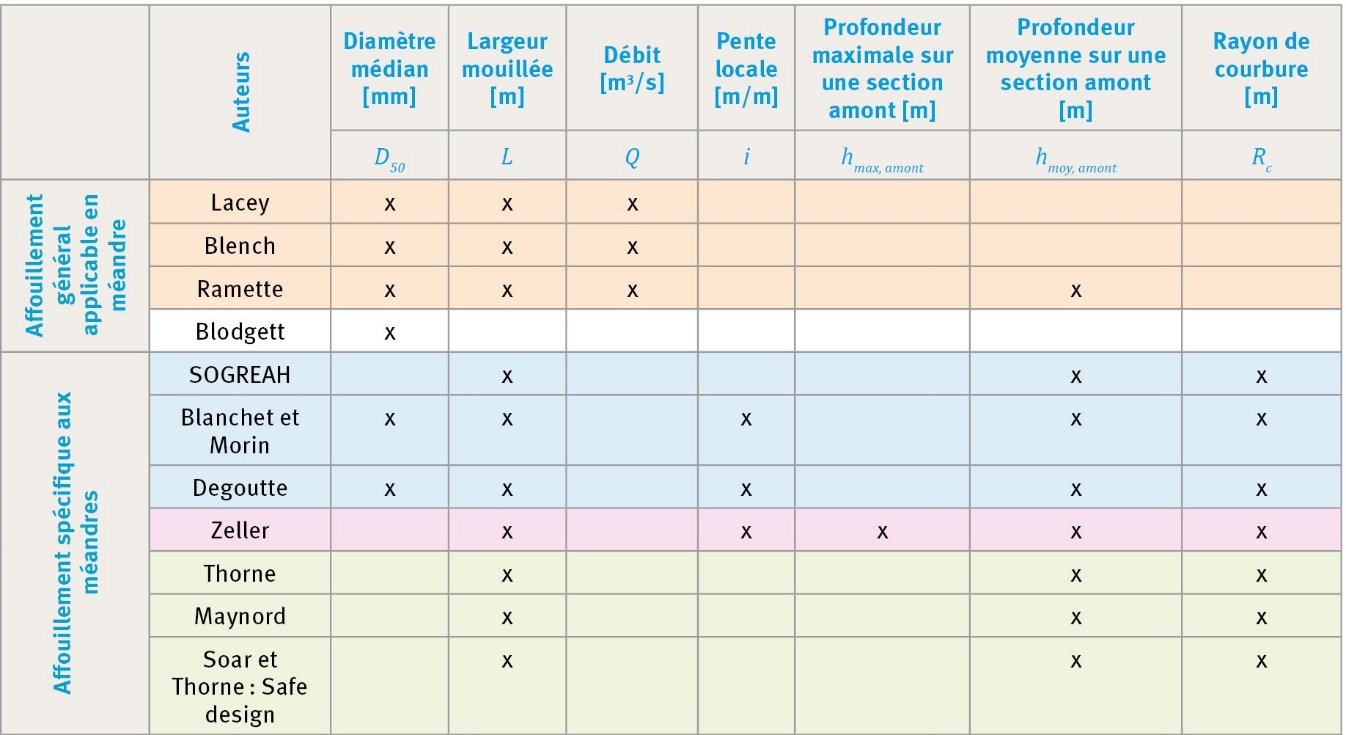
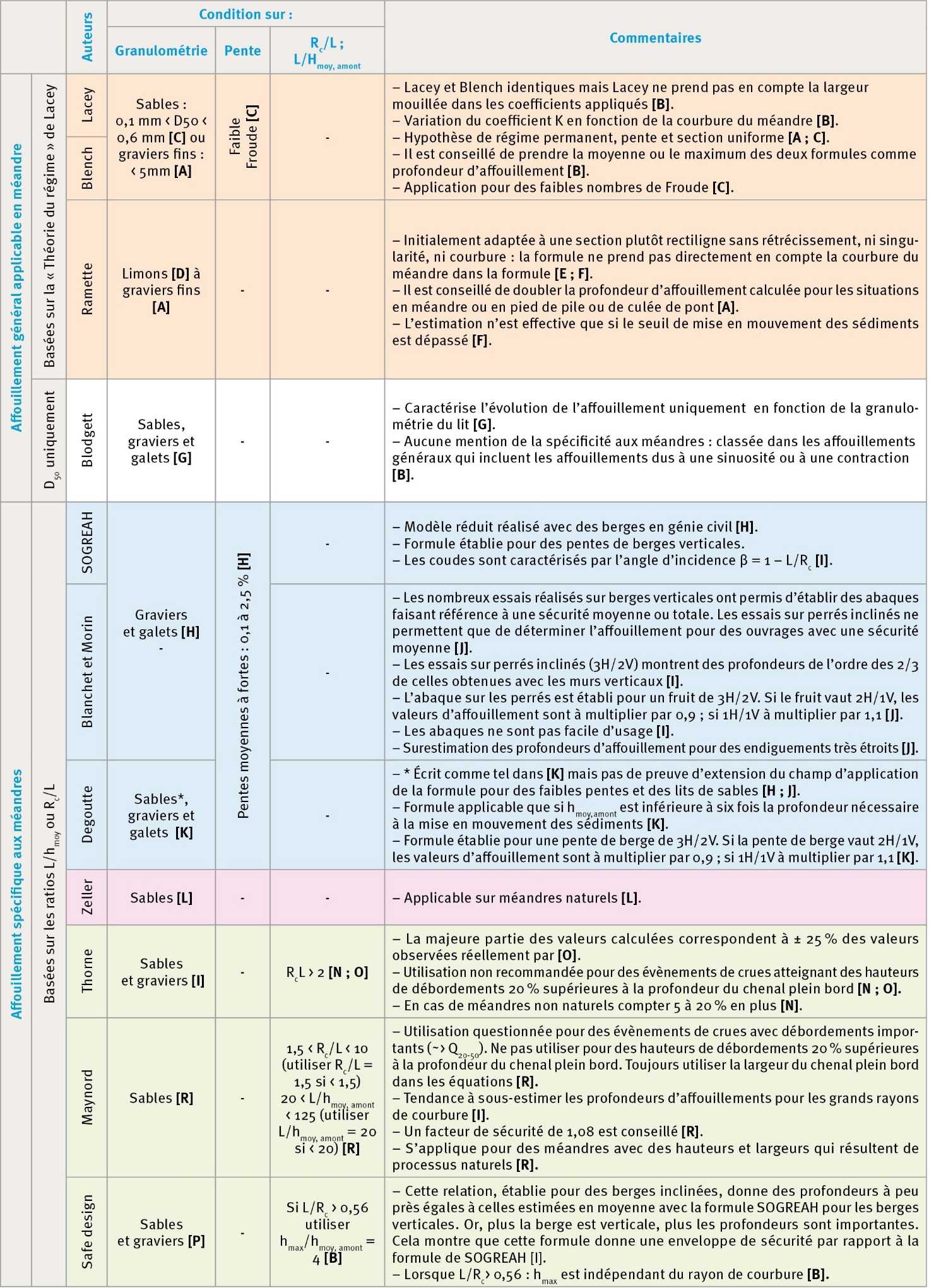
Les formules sont détaillées dans le tableau 2 et prêtes à l’utilisation dans une feuille de calcul associée à cet article (https://doi.org/10.57745/7GW494). Le tableau 3 explicite les abréviations utilisées dans le document et précise les paramètres pris en compte dans chacune des formules.
Cet article n’est pas exhaustif dans les formules présentées pour l’estimation de la profondeur d’affouillement en méandre. Il rassemble les formules retrouvées à plusieurs reprises dans les guides francophones et anglophones traitant du dimensionnement des protections de berge.
Les formules présentées dans l’article s’appliquent aux affouillements en méandre. Certaines formules, classifiées dans la littérature pour le calcul d’un affouillement général, sont tout de même citées car : elles peuvent être ajustées pour les méandres (Lacey et Blench) ; elles s’inspirent de formules applicables aux méandres (Ramette) ; ou il est défini pour la formule que la sinuosité joue un rôle majeur dans l’affouillement général (Blodgett).
Le coefficient K des formules de Lacey et Blench n’est pas adimensionnel et sa valeur varie selon la forme du méandre. Les valeurs proposées en unités SI et US par (USDA et NRCS, 2007b) ne donnent pas les mêmes résultats de profondeurs d’affouillement. Il est donc préférable d’appliquer ces deux formules avec les unités US pour l’ensemble des paramètres sauf pour le D50 qui doit être en millimètres. Pour une application de la formule directement en unités SI, il est conseillé d’utiliser les valeurs du coefficient K recalculées dans le cadre de cet article à partir des valeurs US (tableau 2).
Domaine d’application
Les formules énumérées sont applicables à différents domaines de validité synthétisés dans le tableau 4.
- Les formules de Lacey et de Blench sont applicables à des lits de sables présentant une certaine homogénéité morphologique et une pente relativement faible (faible nombre de Froude). Le même domaine de validité peut à priori être appliqué à la formule de Ramette. Les éléments fournis dans la littérature sont toutefois trop peu précis, voir divergents, ne permettant pas de comprendre clairement la façon dont les équations et les coefficients associés ont été déterminés : sur une section rectiligne et uniforme, au droit d’ouvrages, en fonction de la courbure du méandre ou de la granulométrie ?
- La formule de Blodgett est sans domaine de validité spécifique et prend pour seul paramètre d’entrée le diamètre moyen des sédiments.
- Les formules de SOGREAH, Blanchet et Morin et Degoutte ont été développées pour la conception d’aménagements en génie civil avec des berges pentues, rigides et peu rugueuses. Ces formules s’appliquent typiquement aux rivières de piémonts et montagnes dont le lit est constitué de graviers ou galets. Elles prennent en compte le fruit de berge dans l’estimation de la profondeur d’affouillement et indiquent que l’affouillement est augmenté par des berges plus raides.
- La formule de Zeller est à priori adaptée aux méandres naturels et aux lits de sables. Elle aurait été développée sur des considérations analytiques et des hypothèses sur la distribution de la puissance spécifique dans le méandre.
- La formule de Thorne et la formule Safe Design sont applicables aux lits de sables et de graviers alors que celle de Maynord est préférée uniquement pour les lits de sables. Aucune condition sur la pente n’est explicitement précisée pour ces trois formules. En revanche ces dernières ont un domaine de validité défini par des ratios rayon de courbure sur largeur (Rc/L) spécifiques.
Quelques ordres de grandeur
Plus le rapport hauteur d’eau sur diamètre médian des sédiments est grand et plus la berge est stabilisée et verticale, plus les courants secondaires se développent verticalement et donc plus l’affouillement est profond (Blanchet et Morin, 1990 ; Julien, 2018 ; Leblois et al., 2024). Les profondeurs d’affouillement maximales sont retrouvées dans des méandres où le ratio rayon de courbure sur largeur (Rc/L) est compris entre 2 et 4 avec une tendance maximale autour de 2 (Thorne, 1997 ; Julien, 2018).
Afin d’avoir un repère homogène, les profondeurs d’eau exprimées dans ce paragraphe sont relatives au niveau de crue morphogène, qui correspond au plein bord (compris entre Q1 et Q5). D’après Bagnold (1960), les profondeurs d’eau maximales dans le méandre (hmax, morpho) peuvent atteindre jusqu’à trois fois la hauteur d’eau moyenne estimée dans une section amont au méandre (hmoy, amont, morpho). À titre d’exemple, Thorne (1997), sur la Red River, a observé que ; pour de grands méandres (Rc/L > 10) hmax, morpho vaut entre 1,7 et 2 fois hmoy, amont, morpho ; pour des méandres plus resserrés (2 < Rc/L < 4), hmax, morpho vaut entre 2 et 4 fois hmoy, amont, morpho.
Quelques préconisations pour le génie végétal
Le génie végétal repose sur l’usage de végétation dans des ouvrages dont la capacité à stabiliser les talus augmente avec le temps et la croissance végétale. La reprise de la végétation est donc essentielle au succès de l’ouvrage. L’érosion des matériaux causée par l’affouillement sous le niveau le plus bas de reprise de la végétation (encadré 2), c’est-à-dire sous l’ouvrage végétalisé de génie végétal est ainsi doublement contraignante pour la stabilisation du talus : déstabilisation directe de l’ouvrage par réduction de son ancrage et impossible reprise de la végétation.
Si le site d’étude est soumis à l’affouillement en méandre, il faut estimer la profondeur de cet affouillement en réalisant une analyse hydromorphologique de terrain qui vient appuyer l’estimation obtenue par l’utilisation des formules adéquates. Si cette profondeur menace la partie vivante de l’ouvrage et la stabilisation du talus, la mise en œuvre de structures complémentaires sous le pied de berge végétalisé est indispensable : enrochement ou bois mort (i.e. qui n’a pas vocation à reprendre comme la partie émergée).
Ces structures sont positionnées en dessous de la ligne de plus basse reprise de la végétation ligneuse, (encadré 2). Elles permettent de réduire les affouillements : (1) en protégeant les matériaux via des structures longitudinales (fascine morte, troncs, enrochements, peignes, matelas de souches) ; (2) en repoussant et perturbant les courants principaux et les écoulements hélicoïdaux de façon plus ou moins prononcée selon l’emprise dans le chenal de la structure (épis, souches ou troncs protubérant dans la fosse d’affouillement) ; (3) en combinant ces possibilités. La profondeur d’ancrage de ces structures est à ajuster en fonction des profondeurs d’affouillement estimées pour la crue de dimensionnement.
La ligne des plus bas ligneux est un repère pour l’implantation des ouvrages. Il s’agit du niveau le plus proche de l’eau auquel il peut être attendu un développement de la végétation ligneuse (Baird et al., 2015). En dessous de ce niveau, la présence trop régulière de l’eau ne permettra pas la reprise des éléments vivants. La végétation en place a intégré les variations hydrologiques du cours d’eau et donne la hauteur la plus basse à laquelle il est possible d’installer des ligneux vivants.
Dans le cadre de travaux ponctuels, ce niveau peut être visualisé sur le terrain et reporté lors du chantier.
Dans le cadre de travaux globaux il faut :
(1) Connaître avant travaux par relevé topographique le niveau d’implantation le plus bas en berge de la végétation ligneuse.
(2) Trouver le débit qui correspond à ce niveau soit par connaissances du terrain soit par modélisation.
(3) Projeter par modélisation numérique sur le projet à venir le niveau topographique correspondant à ce débit.
(4) Caler le bas de l’ouvrage vivant à ce niveau.

Fructus, N., Leblois, S., Piton, G., Recking, A., Evette, A., & Pezet, F. (2025). Feuille de calcul pour l’application des formules d’affouillement en méandre. Recherche Data Gouv. https://doi.org/10.57745/7GW494
Remerciements
Les auteurs tiennent à remercier, la chaire OXALIA de la Fondation Grenoble INP ainsi qu’ARTELIA, mécène de cette chaire, d’avoir permis le financement de la thèse de Natacha Fructus et la finalisation de ce travail. Ce travail a bénéficié du soutien de l’Office français de la biodiversité.
_____________________________________
Photo d’entête : © Matthieu Le Dréau - INRAE
Notes
- 1. USDA : United Sates Department of Agriculture ; NRCS : Natural Resources Conservation Service.
- 2. Berge extérieure du méandre, concave et abrupte par opposition à intrados qui est la berge intérieure, convexe et en pente douce du méandre.
Références
- AMEC. (2012). Design guidelines for erosion and flood control projects for streambank and riparian stability restoration. The City of Calgary, Water Resources, Calgary, Alberta.
- Bagnold, R. (1960). Some aspects of the shape of river meanders. USGS Professional Paper. https://doi.org/10.3133/pp282e
- Baird, D. C., Fotherby, L., Klumpp, C. C., & Sculock, S. M. (2015). Bank Stabilization Design Guidelines (SRH-2013-25). Bureau of reclamation, Technical Service Center.
- Bates, P. D. (2022). Flood Inundation Prediction. Annual Review of Fluid Mechanics, 54(1), 287-315. doi:10.1146/annurev-fluid-030121-113138
- Blanchet, C., & Morin, E. (1990). Les affouillements et la protection des berges dans les coudes des rivières à fond mobile. Rapport de synthèse SOGREAH.
- Bonin, L., Evette, A., Frossard, P. A., Prunier, P., Roman, D., & Vale, N. (2013). Génie végétal en rivière de montagne. Connaissances et retours d’expériences sur l’utilisation d’espèces et de techniques végétales : végétalisation de berges et ouvrages bois. 321. https://hal.science/hal-02598614/
- Edmaier, K., Burlando, P., & Perona, P. (2011). Mechanisms of vegetation uprooting by flow in alluvial non-cohesive sediment. Hydrology and Earth System Sciences, 15(5), 1615‑1627. https://doi.org/10.5194/hess-15-1615-2011
- Fructus, N., Leblois, S., Piton, G., Recking, A., Evette, A., & Pezet, F. (2025). Feuille de calcul pour l’application des formules d’affouillement en méandre. Recherche Data Gouv. https://doi.org/10.57745/7GW494.
- Gray, D. H., & Sotir, R. B. (1996). Biotechnical and soil bioengineering slope stabilization : A practical guide for erosion control. John Wiley & Sons.
- Gyssels, G., Poesen, J., Bochet, E., & Li, Y. (2005). Impact of plant roots on the resistance of soils to erosion by water : A review. Progress in Physical Geography: Earth and Environment, 29(2), 189‑217. https://doi.org/10.1191/0309133305pp4
- Jaymond, D., Evette, A., Bray, F., Leblois, S., Jung, D., Vivier, A., & Dorget, C. (2021). BD GeniVeg : une base de données française sur les ouvrages de protection de berges en génie végétal. Sciences Eaux & Territoires, (Articles hors-série 2021), 1-6. doi:10.14758/set-revue.2021.HS.07
- Julien, P. Y. (2018). River mechanics. Cambridge University Press. Cambridge, UK.
- Leblois, S., Evette, A., Favier, G., & Recking, A. (2016). Amélioration des méthodes de dimensionnement des ouvrages de génie végétal en berges de cours d’eau par une approche empirique. Sciences Eaux & Territoires, (Articles hors-série 2016), 1-7. doi:10.14758/SET-REVUE.2016.HS.05
- Leblois, S., Evette, A., Jaymond, D., Piton, G., & Recking, A. (2022). Processus et causes de défaillance du génie végétal pour la stabilisation des berges de rivière : Retour d’expérience sur un large jeu de données issues de la BD GeniVeg. Géomorphologie : relief, processus, environnement, 28(2), 105‑120. https://doi.org/10.4000/geomorphologie.16954
- Leblois, S., Piton, G., Recking, A., Jaymond, D., Buffet, A., & Evette, A. (2024). Riverbank fascines mostly fail due to scouring : Consistent evidence from field and flume observations. River Research and Applications, 41(1), 108-119. doi:10.1002/rra.4356
- Lefort, P. (2018). Morphodynamique fluviale. Approches théorique et expérimentale. Presses Ponts Et Chaussées.
- Matsuura, T. (2004). Stream-bank protection in narrow channel bends using ‘barbs’ : A laboratory study. Doctoral dissertation, Université D’Ottawa. doi:10.20381/ruor-9755
- Odgaard, A. J. (1989). River-meander model. I : Development. Journal of Hydraulic Engineering, 115(11), 1433‑1450. https://doi.org/10.1061/(ASCE)0733-9429(1989)115:11(1433)
- Papanicolaou, A. N., Elhakeem, M., & Hilldale, R. (2007). Secondary current effects on cohesive river bank erosion. Water Resources Research, 43(12). doi:10.1029/2006WR005763
- Somsook, K., Duka, M. A., Olap, N. A., Casila, J. C. C., & Yokoyama, K. (2020). Direct measurement of secondary circulation in a meandering macrotidal estuary. Science of The Total Environment, 739, 139503. doi:10.1016/j.scitotenv.2020.139503
- Thorne, C. R. (1982). Processes and Mechanisms of River Bank Erosion. Dans R.D. Hey, J.C. Bathurst, & C.R. Thorne (dirs.), Gravel-bed Rivers: Fluvial Processes, Engineering and Management (pp. 227-271). John Wiley and Sons Ltd.
- Thorne, C. R. (1997). Channel Types and Morphological Classification. Dans C.R. Thorne, R.D. Hey, & M.D. Newson (dirs.) Applied fluvial geomorphology for river engineering and management (pp. 175-222). John Wiley and Sons Ltd.
- USDA, & NRCS. (2007a). Chapter 6 - Stream hydraulics. Dans National Engineering Handbook, Part 654 Stream restoration Design.
- USDA, & NRCS. (2007b). Technical Supplement 14B - Scour Calculations. Dans National Engineering Handbook, Part 654 Stream restoration Design.
- USDA, & NRCS. (2007c). Chapter 14 - Treatment technique Design. Dans National Engineering Handbook, Part 654 Stream restoration Design.
- Vollsinger, S., Doppler, F., & Florineth, F. (2000). Ermittlung des Stabilitätsverhaltens von Ufergehölzen im Zusammenhang mit Erosionsprozessen an Wildbächen. Studie im Auftrag des Bundesministeriums für Land-und Forstwirtschaft. Eigenverlag Universität für Bodenkultur Wien. Institut für Ingenieurbiologie und Landschaftsbau.
Résumé
Les phénomènes d’érosion sont essentiels au bon fonctionnement des cours d’eau. Cependant, lorsque les enjeux sont importants et non déplaçables, il peut être nécessaire de fixer les berges par des ouvrages de protection. Les techniques de génie végétal, en plus d’offrir une certaine résilience face aux aléas inondations et mouvements de terrain, présentent comparativement au génie civil l’avantage de préserver ou d’améliorer la biodiversité et les services écosystémiques associés. Dans la pratique, ces techniques sont principalement dimensionnées empiriquement à dire d’expert et promues par retour d’expérience. Cette étude s’intéresse au phénomène d’affouillement en méandre, qui est un processus majeur entraînant la déstabilisation de ces ouvrages. Il apparaît donc important de comprendre comment dimensionner la partie inférieure de ces ouvrages. L’analyse de la littérature existante sur le calcul de profondeur d’affouillement a permis de rassembler onze formules offrant chacune une méthode d’estimation particulière. Les domaines d’application de ces formules couvrent un large spectre de contextes hydromorphologiques de rivières pouvant présenter des méandres. L’article présente de façon synthétique les formules répertoriées, leurs genèses, spécificités et limites d’application. Il est complété par une feuille de calcul, disponible en ligne (Fructus et al., 2025), permettant leur mise en application. Les profondeurs d’affouillement estimées doivent toujours être couplées à des observations de terrain et permettent une conception plus robuste et avertie des ouvrages de génie végétal en méandre. Pour limiter les effets de l’affouillement sur les ouvrages de protection de berge, il est ensuite possible d’ajuster la profondeur et la technique d’ancrage en modifiant par exemple la longueur des pieux des fascines ou encore en réalisant des structures de bois mort sous le niveau le plus bas de reprise de la végétation arbustive en berge.
Pas de document complémentaire pour cet article
Statistiques de l'article
 Vues: 5538
Vues: 5538
Téléchargements
 PDF: 140
PDF: 140
 XML: 12
XML: 12

